Why Numbers Have No Meaning
Describing unfathomable abstractions
In the present, there is an almost endless stream of inconceivable numbers bandied about in mainstream conversation. Pundits and politicians talk of the vastness of government budgets or certain individuals’ wealth in millions, billions, or trillions of dollars. Scientists speak in light years or Planck spaces. Environmentalists point to gigatons or parts per million. Technologists calculate gigabytes or terabytes. Even social media influencers count followers in the millions. Everything humans seem to want to quantify measures in amounts of extraordinary size, whether big or small.
Numbers once enumerated readily discernible things: apples in a basket or dollars in a wallet. Some still do, of course, but too often they represent something far more abstract, and far less imaginable. Many numerical terms now employed to quantify things really no longer quantify anything at all. Rather, they serve as nebulous adjectives depicting a range from zero to big to really big, or in the opposite direction to really small. The result is that these kinds of numbers have no meaning.
This is partially hyperbole, of course. These kinds of numbers have meaning to specialists. Depending upon what is studied, the quantities often range so far that there becomes a necessity to employ confusing or opaque denotations. So, in fact, even obscenely sized numbers have value, but comprehending them requires a level of effort that the discourse largely downplays.
Billions
A billion is so commonly used that its immensity often goes unnoticed. The wealth of Amazon owner Jeff Bezos provides a useful example. Bezos currently occupies fourth place on Forbes’ list of the world’s richest individuals. The magazine rates him at a net worth of about $200 billion. The 200 obfuscates the true breadth of the actual quantification. If you break down what it means, Bezos is worth 200 times one thousand million.
Unfortunately, that rendition simply uses more words to vaguely describe something already hopelessly vague. So let’s break it down further.
If your grandfather was old enough to serve in World War II, and then entered the workforce afterward, based on the average American’s salary of the time it would have taken him two hundred and twelve years to earn just one million dollars. Bezos is worth 200,000 times that amount. Put another way, it would have taken your grandfather forty-two million, four hundred thousand years to earn Bezos’ current net worth.
Now the number becomes a bit clearer, but 42.4 million is still excessively big. That is one year for every person living in Afghanistan. But even that is a number without context. Who reading this has been to Afghanistan? And for those who have, what did its overall population look like? Probably pretty sparse—it’s a large, rugged country; certainly not a way to visualize 42.4 million.
Another way to approach it is that this is a larger number than the populace of the most crowded city in the world, Tokyo. While a little easier to envision, it still hardly helps. Someone living in Tokyo obviously knows how jampacked it is, but they never see all the people at once.
To imagine it differently still, the busiest roadway in the United States is Interstate 405 in California. Its average daily congestion comprises 273,186 vehicles. It would take 156 days or about 5 months for 42.4 million cars to travel that length of highway. Bezos’ total net worth would mean one dollar for every car that drives on the I-405 for about 2,006 years—every single day.
Interstate 405; credit Kevork Djansezian/Getty Images via Newsweek.
Here are some other ways to look at Bezos’ total net worth. In the United States, a human can reach an average sufficient daily caloric intake for about 0.50 dollars. At that rate of calories-per-dollars-per-day, Bezos’ net worth could feed every person in the entire world for fifty days. To inoculate everyone in the world against tuberculosis (TB), Bezos would need to spend less than one-quarter of his net worth. TB killed 1.3 million people in 2022—the same as the population of Dallas, Texas or Medina in Saudi Arabia.
Infinities
The purpose of this article is not to criticize billionaires, although once one begins to fathom what wealth a billionaire—one human being—holds it becomes difficult to avoid. Through this criticism, however, the shear volume of a billion becomes a bit more comprehensible. And there are many steps above a billion that enter the public discussion—trillion, quadrillion, quintillion, etc.
Indeed, the American, Chinese, and the next 18 largest national economies are all now measured in the trillions, making any real discussion of them an abstract one to be sure. Even the US state of California’s economy exceeds $1 trillion. Each step up is a thousand times larger than the previous—i.e., a trillion is a thousand times larger than a billion.
But what about numbers with no end? The word we use to describe this concept is infinity. One definition is, “the assumed limit of a sequence, series, etc., that increases without bound.” That seems counterintuitive—a thing without bound that has an assumed limit. Merriam-Webster perhaps does a better job explaining it in plain terms: “unlimited extent of time, space, or quantity.”
The first definition reflects the mathematical conceptualization of the term. A mathematical infinity is one that is measurable, but has no terminal measurement. In other words, one can define any portion of a given set, but not the totality of it. To illustrate, one can measure the seconds in a minute, the minutes in an hour, the hours in a year, the years in a millennium, etc., but one cannot measure the whole concept of time. (This is arguable, but you get the idea).
Infinity can be viewed in the macro world in which humans live both as a truism and a paradox. One can measure time, for example, by segments like minutes or weeks, but the duration of time is infinite while we are alive because it has no measurable end. It is, for our individual intents and purposes, endless (in one direction at least). That is, until life ends. To put it in a philosophical way, our individual existence is infinite because time only exists for us while we live. During that time, it is endless.
But even then, time only ends when measured against that singular existence for that individual. For others, time persists. Thus, for the sum of all living things, time is essentially infinite even if each of their existences is not. It is a truism in the sense that time could conceivably go on forever. (This is a truism in that it is “often presented as true,” despite that some astrophysicists or others might argue that it is is not provably true, or true at all. But all this is an entirely other argument worth addressing elsewhere).
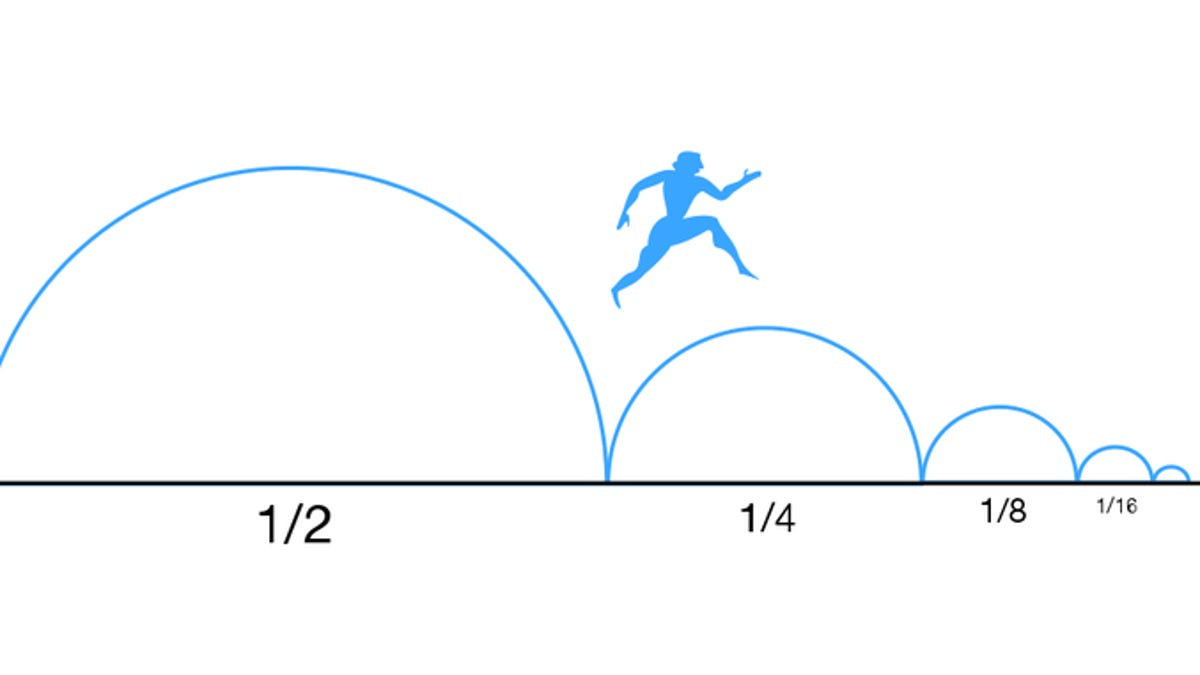
Infinity is paradoxical if one is to apply it to various real-world functions, such as movement. Zeno’s paradox is an example. To walk from home to work, one must necessarily go halfway. Then, to complete the second half of the overall trip, one must walk half the remaining distance. At this point, the walker has reached three-quarters of the way (half of the whole trip, and one-half of the second half of the trip ½ + ¼ = ¾).
To walk the last quarter, the walker must travel another halfway. Now, she has completed ⅞ the distance (½ + ¼ + ⅛ = ⅞). But there is still ⅛ to go, and the walker must cover half of that distance. She travels 1/16 of the total distance (half of the last ⅛), but she is now just 15/16 of the way there. And on it goes without the walker ever reaching the office.
Credit: Quartz.com
Zeno of Elea illustrated the paradox of infinity when applied to real-world movement through a number of scenarios like this. Obviously, the walker will reach her job, but she must cover an ostensible infinity of measured space to do it. From this perspective, infinity seems like a useless tool. The world clearly does not work that way. So, how does such a limitless representation provide any value?
In both math and science (including computer science), infinity offers a useful way to calculate something that either may not have a definable beginning or end, or the beginning or end is so difficult to define or calculate as to near the impossible. A well-known example is a singularity—the center of a galactic black hole. The reason there remains debate about what happens inside of a black hole is that when a star collapses, its mass falls inward compacting to a level of density that exceeds measurement—essentially an area of infinite mass, the singularity.
The anatomy of a black hole; credit: European Southern Observatory (ESO), CC BY 4.0.
Physicists can theorize about what occurs nearly up to the point of singularity, and have confirmed their theories with observation, but the math “breaks down” as one gets really close. In other words, the numbers become so large as to be infinite, with no measurable boundary or notable limit. The math provides useful information about the structure of the black hole, but only to a point. Rather than try to force an endpoint into the equation, they assign a value of infinity because the math sufficiently explains the processes at work up until those very extreme numbers.
This methodology can apply to any calculation of vast or unending series or sums of numbers when demarking the endpoint is unnecessary. When infinity is applied to a function, it will typically graph in a curve like this:
Credit: Sergejevicz, CC BY-SA 4.0
This graph shows the Lorentz Factor, which is an expression of “how much the measurements of time, length, and other physical properties change for an object while it moves.” We need not explore the details, but these properties become extremely difficult to measure as we approach the speed of light. Rather than try to calculate every value, the far end of the graph can be treated like infinity. Many similar examples abound.
The cosmos
A quick overview of a billion to infinity helps to imagine the enormity of what these ideas represent. One cannot expect to walk away from such a short narrative with a complete conceptualization, but seeing just how expansive even a billion is, one can better grasp the utter vastness of much larger quantifications. And no place better exemplifies incomprehensible sizes than the cosmos.
A key metric for measuring the cosmos is the lightyear. Although many know it, it is useful to remind readers that a lightyear is a unit of distance, not time. It is a term to describe the distance light travels over an earth-based year. The speed of light is 299,792,458 m/s (300,000 km/s; 186,000 miles per second; or 671 million mph) in a vacuum. A lightyear, therefore, is about 5,878,625,373,184 miles (9,460,730,472,581 km).
The closest star to Earth outside the solar system is Alpha Centauri, 4.37 lightyears away. At its fastest speed ever achieved, the space shuttle would require more than 38,342 years to reach there. That many years ago, Homo Erectus and Neanderthals both still walked the land. The fastest manmade machine ever constructed, the Parker Solar Probe, would require 1,700 years to arrive there. Seventeen-hundred years ago, Constantine ruled Rome.
As mentioned, Alpha Centauri is the closest star to Earth besides its own. The observable universe spans 93 billion light years, 19.7 billion times as large as the distance from Earth to its nearest extra-solar-system star. The space shuttle would need more than 759 trillion years to travel that distance, and the Parker Probe 33.5 trillion years.
In effect, ∞.
To put Earth’s place in some perspective of this seeming eternity, James Gearheart explains it:
[L]et’s start by imagining the Milky Way galaxy, which spans about 100,000 light-years in diameter. Now, if we were to shrink the galaxy down to the size of Earth (with a diameter of about 12,742 kilometers), the relative size of Earth itself would become unimaginably small. In fact, Earth would be 742 billion times smaller in comparison — about the size of a single human red blood cell.
Earth would represent a single human blood cell in the body of the Milky Way Galaxy alone. The universe holds anywhere from 100 to 200 billion galaxies, possibly many more. Ethan Siegel offers a logarithmic view of the size of the universe:
Stars are tiny compared to the distances between them. If the Sun were a grapefruit in Seattle, WA, then the next nearest star would be a grapefruit in New York.
But galaxies are not tiny compared to the distances between them. If the Milky Way were a grapefruit in Seattle, WA, then Andromeda — the Local Group’s largest galaxy located 2.5 million light-years away — would be a grapefruit in the same room, only about 10 feet (3 meters) away…
The Milky Way galaxy is big, but it’s only a few tens of thousands of times as big as the distance between any two typical stars. The distance between any two stars is pretty big, but it’s only a few hundred thousand times as big as the Earth-Sun distance. And the Earth-Sun distance is only ~10,000 times as big as the Earth, which is, at last, accessibly-sized to human beings.
This is not the end of the story, however. For, the universe is not static. In fact, everything within it is moving away from everything else, and swiftly. While galaxies can move independently, what is causing the sum of them to move is the expansion of spacetime itself.
As spacetime expands it carries everything embedded in (on?) it along with it. And because spacetime expansion is not restricted by the speed of light (for reasons worthy of a separate discussion), the sum effect is that galaxies are moving away from each other at speeds faster than light. As the universe expands, the number of galactic entities we will be able to see will eventually diminish as each moves beyond the ability of its light to reach us.
From super big to super small
Just as these gigantic numbers boggle the mind, so too do very small ones. The smallest figure scientists use is the Planck length. Named for German physicist Max Karl Ernst Ludwig Planck (1858-1947), Planck units are “based on the speed of light, Newton’s gravitational constant, and Planck’s (reduced) constant.” Roughly speaking, this number is calculated at 10-35 meters. To compare, an electron’s radius is about 10-22 meters. Thus, a Planck length is nearly ten trillion times smaller.
The Planck unit is perhaps the most precise method of depicting measurement because it relies on universal constants, not somewhat more arbitrary units such as meters or feet. As Max Planck himself put it, “These necessarily retain their meaning for all times and for all civilizations, even extraterrestrial and non-human ones, and can therefore be designated as 'natural units’.” The reason it is so small is that it is the simplest unit at which quantum mechanics becomes relevant. In other words, there could be smaller units, but scientists have no known conceptual framework by which to identify or apply them.
Moving up the scale are subatomic particles. The smallest of them depends upon the standard used to characterize them—diameter or mass. For mass, the tiniest non-zero mass particles are neutrinos. Describing them is difficult—trillions pass through the human body every second with such negligible mass that even this extraordinary number of them goes unnoticed. Electrons weigh 500,000 times more than neutrinos, about 9.11 x 10-31 kg—again, an inconceivably miniscule number. Protons and neutrons, along with electrons, make up atoms.
An atom’s nucleus is much larger, yet compared to things in the macro world, they too are unimaginably small. To illustrate, the “atomic nucleus is as small to a virus as a virus is to us.” A man weighing 70 kg (154 pounds) consists of approximately 7 x 1027 atoms—or seven billion billion billion atoms. This is roughly 7 octillion atoms:
7,000,000,000,000,000,000,000,000,000
That is 70,000,000,000,000,000 times more than Bezos’ net worth.
Recall that the size differential between a virus and an atom’s nucleus is comparable to the difference between a human and a virus. The largest viruses average around 300 nanometers (nm) long. Bacteria are about 6 times larger. A single bacterium weighs on average, about one picogram. One gram is equal to 1,000,000,000,000 picograms. Thus, 70,000,000,000,000,000 bacteria would equal the weight of a single average-sized man, as would six to six hundred times that number of viruses.
When one examines the virtually infinite bulk of the universe and the equally robust smallness of the quantum-level cosmos, the size of humanity’s physical existence suddenly seems quite limited.
Data
Before we discuss why any of this matters, it is necessary to address the driving measurement of modern society—data. The majority of devices today operate in megabytes and gigabytes. These are values denoting collections of the most basic measurement of data—the bit. A bit—or binary digit—is the expression of a logical state of information, often positive/negative, on/off, or true/false.
Bytes are a collection of eight bits. These are actually represented in halves—nibbles—and look like this: 0010 0000 (each grouping of four is a nibble, and the two together is a byte). Kilobytes, megabytes, gigabytes, etc., represent increasing orders of magnitude.
As seen in the table, these are not represented in factors of 10. The reason for this is because bits are a factor-2 system. When multiplied exponentially, the result will always be a multiple of 2, but not necessarily a multiple of 10. For purposes of imagining these totals, however, we typically round off. Thus, one KB equals about 8,000 bits. One MB is 1,000 KB or 8 million bits. A GB is about 8 billion bits, etc.
Like government budgets or billionaire wealth, the numbers quickly become insanely large. In 2023, new cell phones contained storage averaging between 128 and 256 GB. That same year, new phones sales neared 1.4 billion. For 2023, then, the available data storage on new phones alone reached 179,200,000,000 GB at the lowest, or 179,200 petabytes. If rendered in bits, that is about 1,436 followed by seventeen zeroes.
The total amount of digital data stored across the world is many magnitudes larger still. It is so large, in fact, that data scientists currently measure it in zettabytes—1 sextillion bytes.
Global data volume in zettabytes. Credit: Statista.com
Why is there so much?
In a single day,
we generate 500 million tweets, 294 billion emails, 4 million gigabytes of Facebook data, 65 billion WhatsApp messages and 720,000 hours of new content added daily on YouTube.
Add to that the various backend processes for artificial intelligence, database administration, cybersecurity, not to mention the many other social media platforms out there generating user-supplied data, and it is easy to ponder how data volume multiplies so swiftly.
To try and apprehend this amount, if each bit of data expected to be generated in 2025 is represented by a one Euro (£1) coin laid flat, the stack will extend 250 times farther than Alpha Andromedae is from Earth, or around 2,550 lightyears. According to one study, if global data continues to grow at the rate it has over the past 10 years, “[in] about 110 years from now, the power required to sustain this digital production will exceed the total planetary power consumption today.”
In other words, without major recalibrations in how we store data, generate electricity, or both, this digital world will come to a screeching halt in the lives of our grandchildren.
The takeaway
Because so much of the discourse surrounding critically important or politically charged subjects invokes numbers like these, it is crucial that we have some ability to understand them. When a news outlet reports that the US military defense budget of 2023 was $816.7 billion, for instance, this on its own has limited value. When you realize that that amount could feed the entire world for roughly 220 days, the amount assumes a more profound significance.
The US military budget of a single year, could feed every child in the country between birth and 19 years-old for 54 years. It would cost 0.005% of the annual military budget to feed every American child each year (at approximately 2,300 calories per day).
Whether you are thinking about government budgets or travels to the stars, wrapping your head around these huge amounts is a necessity to truly grasp the concept. It also plays an integral part of devising solutions. How can one calculate, for example, the potential impact on the availability of drinking water without knowing how big a gigaton is? After all, glacial loss—which supplies water sources for billions of people—is now calculated in these amounts.
The Himalayas lost 174 gigatons of glacial ice each year between 2003 and 2009. A gigaton is one billion tons. Meredith Nettles, Professor of Earth and Environmental Sciences at Columbia University, provided a useful image to visualize the size of a single gigaton. Glacial loss in the Himalayas alone has exceeded 3,480 times this amount in the last two decades.
Source: storybook.com
Next time you hear such numbers, think about some of these comparisons. It is harder to be fooled by the enormity of them when politicians or others mention them only casually. When someone promises that anyone can become a billionaire with just a little hard work and a unique idea, remember that if you are earning around $75,000, it will take you more than 13,300 years to earn your first billion if you can manage to save every dollar earned.
If people suggest that it would be easier to terraform and settle another planet, remember that the closest possibility—Mars—is 33.9 million miles away (at its absolute shortest distance). At the current state of fuel consumption for the most efficient rockets able to move humans, the price would be $393 billion at the lowest, and could exceed $780 billion just for gas. That does not account for all the related mission costs, and some have reported that fuel comprises as little as 1% of the total—probably even less since we do not yet know how terraforming would even work.
As the world grows in virtually every metric—whether population, digital data, dollars, or otherwise—these numbers will become ever more deeply entrenched in the lexicon. If we cannot find a way to fathom their meaning, our reality will fall even farther from our grasp than it already has.
To read about conducting IT help-desk fixes on a device located billions of miles away, click the link below.
Finding Voyager
It is, perhaps, one of the loneliest machines in existence. Hurdling through the cosmos, some 15 billion miles away from home, Voyager 1 is older than many of the people reading this. It launched before cellphones came into common use, and even makes the Windows Operating System