Is a Warp Drive Engine Really Possible?
Here's what real physicists say about it.
Theoretical Physicist Miguel Alcubierre published an idea in 1994 for a solution that could allow for faster-than-light travel. Alcubierre’s idea, often referred to as a “drive,” similar to the “warp drives” depicted in Star Trek, actually constitutes a physics principle more than a mechanized engine. Put simply, the Alcubierre drive proposes stretching the fabric of spacetime in a wave, causing a contraction ahead of the vessel and an expansion behind. The “bubble” in between can exceed the speed of light while simultaneously insulating the passengers and craft inside of it from the usual artifacts associated with approaching lightspeed.
Ok, there is a lot to unpack there. So, let’s start with some basics.
The Speed of Light as a Speed Limit
It was not until 1975 that physicists finally agreed upon the actual numeric value of the speed of light—299,792,458 meters per second in a vacuum. That figure gets complicated under different conditions. In a vacuum it remains constant, so scientists use that constant as a standard for both distance and time. A meter, for instance, is 1⁄299792458 of the distance traveled by light in a vacuum in one second.
A particular—and arguably the most important—feature of light is that its speed remains constant irrespective of the observer. Best articulated in Albert Einstein’s Special Theory of Relativity, unlike the speeds of other things, light’s speed is not affected by its motion or the motion of its observer(s). Einstein wrote (translated to English): “light is propagated in vacant space, with a velocity c which is independent of the nature of motion of the emitting body.” [You can read Einstein’s full paper, titled “On the Electrodynamics of Moving Bodies” in its English translation here.]
Where it becomes confusing is in the context of relativity. To understand relative speeds, it is useful to think of a person walking through a train that is also moving in the same direction. To people on the train, the person appears to be walking at normal speed, say 3 or 4 mph. But to an observer outside, the person is moving at the speed of the train plus the speed at which they are walking.
Light’s speed, however, does not vary no matter who or where the observer or the emitter is relative to each other. What changes is the distance or the time based on the observer’s frame of reference. Because the constant among these units is only the speed of light, it has been referred to as the conversion factor that unites them. Stephen Reucroft and John Swain, professors of physics at Northeastern University in Boston, Massachusetts, explained Einstein’s theory this way:
[I]n some sense, space and time must be the same, despite our habit of measuring space in meters and time in seconds. But if time and space are similar to the extent that they can be converted one into the other, then one needs some quantity to convert the units—namely, something measured in meters per second that can be used to multiply seconds of time to get meters of space. That something, the universal conversion factor, is the speed of light.
In other words, the speed of light is an observable, measurable phenomenon as well as a mathematical tool to convert two distinct mathematical units—space and time. As such, the speed of light is generally treated as a mathematical constant, a value that doesn’t change even though experiments have shown that the speed of light does indeed vary depending upon the medium through which it passes.
The speed of light through a vacuum is treated as not just a constant, but also the speed limit of any particle in the universe. Most people have at least heard of Einstein’s famous equation: E = mc2. The equation states that the amount of energy in an object is equal to the relativistic mass of the object times the speed of light squared. Nova explains that energy and mass, according to Einstein’s equation, are interchangeable.
The term “relativistic mass” is a bit confusing, even though it is frequently invoked in this topic of discussion. In short, as one approaches the speed of light, the physics derived from classical equations break down. Einstein’s theory solves those insufficiencies by accounting for variations in distance and time. This is particularly important when it comes to massless particles. In any event, a warp drive assumes the movement of a rather massive entity—a spaceship—so we need not stress much over the intricacies of relativistic principles related to massless bodies.
Instead, let us operate under the rudimentary version of understanding—that as an entity with mass approaches the speed of light, the energy necessary to accelerate it further becomes immense, and eventually infinite. Look at it this way:
In E = mc2, we are looking for the value of E—the energy. Let’s suppose we are converting a gram of water into energy. According to Einstein’s calculation, the result would be 89,875,517,873,681,764 joules. This is the energy yield of some nuclear weapons.
As noted above, mass and energy are interchangeable. So really, mass is simply a measurement of how much energy there is in an object. When talking about acceleration, such as in an effort to reach the speed of light, there is also energy associated with motion. The “E” in Einstein’s equation is therefore the result of the object’s rest mass combined with its energy of motion times the constant c squared.
To sum all this up, then, the problem is that any object with measurable mass requires exponentially increasing amounts of energy to accelerate the closer it gets to the speed of light. That amount of needed energy rises to the point that the value becomes, for-all-intents-and-purposes, infinite, which is why the speed of light is considered the universal limit. In fact, the limit for a body with mass is an increment below the speed of light because the energy needed to reach it becomes infinitely high.
Manipulating Spacetime
Since we know that simply plunging ahead toward the speed of light pushed by some super-charged engine will never be sufficient to reach—never mind surpass—the speed of light, physicists took a different approach: Warping spacetime. This allows faster-than-light travel without violating the fundamental rules of physics described above. But what are they talking about?
Spacetime describes a single framework combining the three dimensions of space—length, width, and height—with time. It is complicated to envision. As Paul Sutter wrote, “Einstein made a beautiful machine, but he didn't exactly leave us a user's manual.” Indeed, physicists do not agree on what spacetime is themselves. Daniele Oriti of Ludwig Maximilian University of Munich in Germany described it like this:
The atoms of space are not the smallest portions of space. They are the constituents of space. The geometric properties of space are new, collective, approximate properties of a system made of many such atoms.
His is perhaps a more eloquent articulation of the relationalism principle in which space comprises a pattern of correlations among objects. String theorists suggest that correlations between objects might start at the quantum level, through entanglement. Time too, they contend, could emerge this way.
Those from the loop quantum gravity camp describe a similar “emergent” theory as the string theorists. Except, where the string theorists view a collective of entangled particles acting in no particular agreed-upon rhythm that nonetheless emerge into a consistent representation, loop quantum gravity suggests that the emergence occurs precisely because of a coordinated rhythm among particles even if individually they share no similarity to their final representation.
In other words, for string theorists spacetime is merely the canvas or background upon which the physics “happens,” while for loop quantum gravity theorists spacetime is made up of its own unique, fundamental units.
This is how spacetime is often depicted, showing the curvature of it from the influence of gravity of planetary and other bodies. Source: Caltech
In either case, spacetime is the representation of the “thing” that emerges not just from its component parts, but from the necessary and predictable interactions of them. Take water as a more down-to-earth example.
Water is made up of H2O molecules, which themselves are made up of individual particles, (Hydrogen and Oxygen), which themselves are made up of… well you get the point. At its most basic component part, a single proton for example, the term or idea of “water” is meaningless. But, as the component parts come together, eventually their relationship behaviors form the wet, flowing medium we recognize in the macro world. The unpredictability lies at the component-part level, whereas the final representation is more readily observable and thus understandable.
So how, then, does one propose to manipulate spacetime, which cannot even be explained? For Alcubierre, the answer was math. He simply sought to determine if the conception was mathematically possible. First, he provided quantitative values for the “geometry” of spacetime. This geometric rendering included “hypersurfaces.” Put as simply as possible, a hypersurface is an analog of a n-dimensional surface in a n+1 dimensional space. It is an algebraic simplification or generalization of any ordinary surface in a dimension of one value higher, for example of a 2-dimensional surface in a 3-dimensional space. Alcubierre calculated the necessary metric for defining these surfaces. Here is the Anderson Institute’s breakdown:
Where α is the lapse function that gives the interval of proper time between nearby hypersurfaces, βI is the shift vector that relates the spatial coordinate systems on different hypersurfaces and γij is a positive definite metric on each of the hypersurfaces. The particular form that Alcubierre studied is defined by:
Where:
And:
With R > 0 and σ > 0 arbitrary parameters. Alcubierre's specific form of the metric can thus be written;
So, what does all of this mean?
Alcubierre’s paper exhibited the mathematical basis for a structure that essentially squeezes through the fabric of spacetime. Crucially, the interior of the bubble remains undisturbed by its passage through space, sort of similar to the way we hurdle through space on Earth but do not really feel or even notice the effect because we are insulated within our atmosphere. The bubble itself, however, can effectively exceed the speed of light because it is “surfing” along spacetime, not passing through it.
What’s peculiar about Alcubierre’s computations is that he determined spacetime’s metrics first, then calculated the stress-energy-momentum-tensor value, which is something like figuring out the energy density values and momentum. In effect, Alcubierre ran Einstein’s field equation in reverse.
In so doing, the bubble does not violate the speed of light restriction because it is not moving in the traditional sense. Michael J. Pfenning and L.H. Ford describe it this way:
[T]he proper time of the space going traveler’s trip is identical to that of the elapsed time on earth. However, the spaceship never locally travels faster than the speed of light. In fact, the spaceship can sit at rest with respect to the interior of the warp bubble. The ship is carried along by the spacetime, much in the same way that the galaxies are receding away from each other at extreme speeds due to the expansion of the universe, while locally they are at rest. The warp drive makes use of this type of expansion (and contraction) in order to achieve the ability to travel faster than light.
Travelers therefore ride along in what to them seems a stationary object, but from the perspective of an outside observer the craft whisks away in an instant. The trip would take, in Alcubierre’s view, “an arbitrarily small proper time,” a period experienced identically by the travelers and any adjacent observer. In other words, the travelers could jet off to some distant galaxy and back to Earth without experiencing time dilation and the associated twin paradox.
Can we turn the math into a viable machine?
Unfortunately, here we must apply the brakes. Professor David Kipping wonderfully explains that the problem is not really one of physics. Rather, it is an engineering problem… an extremely difficult or even impossible engineering problem. The first issue is energy.
Michael J. Pfenning and L.H. Ford calculated that to generate a bubble of sufficient size that it could contain a human-loaded vessel, the required negative energy is “unphysically large.” Chris Van Den Broeck argues, however, that by modifying the Alcubierre metric just slightly, the energy requirements can be diminished to a “few solar masses.” Still, a single solar mass is equal to 2×1030 kg. Remember that mass and energy are interchangeable, so a single solar mass comprises an extraordinary amount of energy, and Van Den Broeck’s plan requires a few such masses.
Relatedly, Alcubierre’s proposal requires negative energy (or negative mass). Such negative energy violates the Weak Energy Condition (WEC), an issue Alcubierre himself noted. Scientists estimate that about 70% of the universe consists of negative-pressure energy, also called “dark energy.” WEC demands that similarly situated observers (as in, those moving forward together in time) must see a positive energy density. Violating this condition necessarily requires the presence of dark or negative energy, but scientists have not yet identified or observed any such particle. Some do not agree one exists at all.
It seems that no currently configured warp drive can avoid violating the WEC or the related Null Energy Condition (NEC), although one physicists claims otherwise—but, more on that below. The NEC “requires that the average along a complete, achronal null geodesic of the stress tensor, projected onto the geodesic, is non-negative.” Alternatively put, the NEC does not allow the net energy density of a certain region of space to be negative.
Jessica Santiago, et. al., argue that to successfully build a physical warp drive, one must overcome the violations of the WEC and NEC. They propose the following as options: (i) modify the theory of gravity, (ii) modify the definition of warp drive, (iii) modify the energy conditions, (iv) appeal to macroscopic quantum physics, or (v) allow for singularities or CTCs (time travel). They point out that none of these provide reasonable solutions.
Erik W. Lentz posits in a recent paper that he has found a solution to the warp drive that does not violate the WEC or NEC. Lentz describes it this way:
Hyper-fast (as in faster than light) solitons within modern theories of gravity have been a topic of energetic speculation for the past three decades. One of the most prominent critiques of compact mechanisms of superluminal motion within general relativity is that the geometry must largely be sourced from a form of negative energy density, though there are no such known macroscopic sources in particle physics. I was recently able [to] disprove this position by constructing a new class of hyper-fast soliton solutions within general relativity that are sourced purely from positive energy densities, thus removing the need for exotic negative-energy-density sources. This is made possible through considering hyperbolic relations between components of the space–time metric’s shift vector. Further, these solutions are sourceable by a classical electronic plasma, placing superluminal phenomena into the purview of known physics.
Santiago et. al. point out, however, that Lentz “assert[s] the existence of one sub-class of timelike observers for which the energy density is positive. This is not enough to show that the WEC is satisfied.” As noted above, the NEC prohibits the net energy density of a specific area of space from having a negative value.
Likewise, the WEC demands that similarly situated observers (those moving forward together in time) see a positive energy density. Santiago and team argue that Lentz ignores some similarly situated observers in his calculation, a dismissal not allowed by the WEC.
Lentz produced a rebuttal to this opposition, but the best he could argue for a solely positive-density energy source still requires many solar masses’ worth of energy. And even to achieve that milestone, he notes that none of the known methods are possible without invoking some negative energies. He writes:
Extreme energy savings is going to be necessary – tens of orders of magnitude – to bring the energy required for a warp drive down to a level that can be tested in a laboratory setting let alone be considered a viable transportation technology… There exist numerous techniques for reducing the energy requirements of the Alcubierre solution, several of which have been very successful in reducing the (magnitude) energy requirements of the system in excess of thirty orders of magnitude… Unfortunately, each one of these methods in their presented forms require negative energies themselves. [Citations omitted]
In effect, Lentz’s solution—while certainly accomplishing the reduction of energy needed in the Alcubierre model—still falls short of anything reasonably buildable without resorting to methods that violate the WEC and NEC.
Alcubierre himself pointed to another problem in his own design, one he termed the “Horizon Problem.” He wrote, “an observer on a spaceship cannot create nor control on demand an Alcubierre bubble.” Anyone inside the bubble cannot create or effect any energy outside the bubble.
What this means is that even if it were possible to create the bubble and send it along its way, the inhabitants inside would have no means to direct it or even stop it. Professor Kipping explains that to control the path of the bubble, we would need some sort of infrastructure external to the bubble akin to an “interstellar highway.” This highway would require negative field generators all along the path of the bubble in order to properly steer it to and stop it at its destination. How humanity could ever achieve this remains unknown.
As in all discussions of interstellar travel, the question of what to do about radiation also arises. During its travel, the Alcubierre bubble will generate Hawking Radiation along its rim. The result, as concluded by Stefano Finazzi et. al., is “that the Hawking radiation in the center of the bubble will burn the internal observer with an excruciating temperature of TH ∼ κ ≥ 10−2 TP, where TP is the Planck temperature, about 1032 [Kelvin].” This temperature is that at which “physicists believe all matter starts to break down.”
Finazzi and his co-authors reached a grim assessment for faster-than-light travel: “we think that this work is casting strong doubts about the semiclassical stability of superluminal warp drives.” While increasing the thickness of the shell around the bubble would help reduce this temperature—though perhaps never sufficiently for survival of the travelers—it is no small problem to change the shell’s thickness.
Alcubierre’s math suggests the shell cannot exceed a thickness of more than a few Planck lengths. A Planck length comprises the smallest measurable unit in the entire universe. Put another way, “the Planck length is the length-scale at which quantum gravity becomes relevant.” The actual number is 10–35 meters—an inconceivably small figure.
To make the shell any bigger, Pfenning and Ford posit that the velocity of the bubble needs to be severely increased. Unfortunately, for every order of magnitude the velocity increases, so too must the energy increase. An increase of even a single order of magnitude stretches the energy requirements into the realm of impossible, whether employing positive or negative energy.
Finally, perhaps the most insurmountable problem of all has been called the catch-22 flaw. D. H. Coule wrote that “one needs to transcend the speed of light in order to construct the warp drive in the first place.”
Physicists Bobrick & Martire told Scientific American that “none of the physically conceivable warp drives can accelerate to speeds faster than light” without first being able to accelerate particles outside the bubble to such speeds. Professor Kipping observed that no one has proposed a solution for how to even begin building the bubble without attaining faster-than-light speed for these external particles.
The reasons for this are complex, but physicists simply have not conceived of an alternative hypothesis for how to create the necessary conditions for forming the bubble without relying upon particles outside of the bubble moving at faster-than-light speed. Therefore, the theoretical construction itself is burdened by this catch-22, which means we are very far away from actual construction.
(Of note, the phrase catch-22 is coined from a book by the same name written by Joseph Heller. The phrase derives from certain paradoxes presented in the book.)
Image source: Nick Weatherhead
Conclusion
There are actually two distinct questions with which physicists grapple concerning warp drives. First, is warp drive possible? The short answer appears to be yes. While it is laden with numerous problems, the concept of faster-than-light travel seems to fit within the rules of physics and the current conceptions need (substantial) tweaking more than entire reconstructions. The real problem lies in the second question. Is it feasible at the macro level?
To that, the answer seems to be no—at least not anytime soon, if ever. To date, scientists have not been able to produce a scenario in which they can accelerate a single particle to faster-than-light speed. Doing so on the macro level, (i.e., in the form of a manned spacecraft) provokes so many more problems that it may prove intractable enough that scientists will simply deem it impossible.
The human body does not accommodate extreme forces well, and the various factors involved in accelerating one to warp speed certainly entail the application of extreme forces. Thus, the obstacles do not reside merely in the physics of acceleration and maintaining travel speed, but also in insulating travelers from the various mechanisms by which the universe will try to kill them for attempting to break its law.
* * *
I am the executive director of the EALS Global Foundation. I am also the managing director of the Dharma Farm School of Translation and Philosophy.
If you like my work, you can also follow me at the Evidence Files Medium page for an exploration of law, politics, history, and social issues; or Buy me a Coffee as a small show of support.
For another article exploring space, see below.





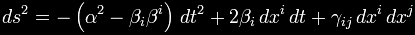



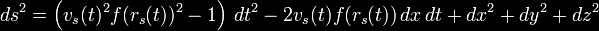


Perhaps we are limited to creating a warp drive on earth and we need experiments in space .. like the way metal fuses to itself in space. There is a different set of how things work there. I was hoping we were closer to building it then we are. Great article. 5 star ⭐⭐⭐⭐⭐